Understanding Earthwork Volume and Isochore Calculations
In the Earthwork Report, surface to surface (and surface to elevation) volumes are calculated by computing the isochore between the surfaces (or between the elevation and surface) using the prismoidal method. First, each point is projected onto the other surface. Then, the corresponding elevation is interpolated, and the elevation difference is stored with the generated isochore point. The breaklines of both surfaces are used to generate isochore breaklines in a similar manner. Additional points are inserted into the isochore breaklines where they cross the surface triangles.
A Triangulated Irregular Network (TIN) is generated to represent the surface created by the isochore points and breaklines. The isochore represents the thickness, or difference in elevation, between the two surfaces. The software generates the surface triangles for the isochore by linking the isochore points, while honoring all breaklines and points common to both surfaces.
The triangulated isochore is used to determine the volumes by breaking the data for each triangle into the appropriate number of truncated vertical prisms. If the three points of a triangle all have positive or all have negative elevations (all fill or all cut) then a single triangular prism is present, as shown in case 1.
Case 1: All Excavation

If the isochore triangle has both positive and negative elevations (cut and fill), then the triangle is broken into additional triangular prisms such that each prism represents only cut or fill, as shown in case 2.
Case 2: Partial Excavation and Partial Fill
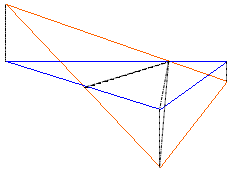
The volume of each prism is equal to the average height (i.e. isochore elevation) times the planimetric area. The total fill volume for the isochore is the sum of all positive prismoidal volumes. The total cut volume is the sum of all negative prismoidal volumes.
This method is considered more accurate than cross-section average end area or grid methods. The differences obtained between methods depend on the size of the grid or interval of cross-sections and the irregularity of the surfaces. Smooth surfaces may show differences of less than 1%. Some test cases have shown differences of as much as 10% when the cross-section interval is 15 meters (49.21 feet) and the terrain is rough. Mathematically, as the size of the grid or cross-section interval decreases to a very small value, the volumes of these methods agree with volumes computed from the isochore triangles.
Note: The accuracy of volume calculations is dependent on the accuracy of the data that is used and the surface that is created. If breaklines are not properly used to form a valid surface, good point data can produce bad volumes. If an insufficient number of points are used to describe a surface, then irregularities from the recorded data to the actual ground will produce volumes differing from field conditions.