Typen von Spiralkurven
Die software unterstützt die folgen Typen von Spiralkurven:
| Methode | Länge | Letzte Station | PI |
|---|---|---|---|
| Klothoide |
* |
* |
* |
| Eiklothoide |
* |
* |
– |
| Kubische Spirale |
* |
* |
* |
| Bloss-Übergangsbogen |
* |
* |
* |
| Kubische Parabel (Korea) |
* |
* |
* |
| Kubische Parabel (NSW) |
* |
* |
– |
Die Klothoide wird durch die Länge der Spiralkurve und den Radius des angrenzenden Bogens definiert. Die Formeln für die Parameter x und y lauten für diese beiden Werte wie folgt:
Parameter x:
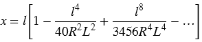
Parameter y:
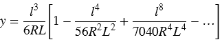
Durch Ändern des Anfangs‑/Endradius für eine Eingangs‑/Ausgangsklothoide von Unendlich in den gewünschten Radius kann eine Eiklothoide (Eilinie) definiert werden.Um den unendlichen Radius wiederherzustellen, wählen Sie im Kontextmenü Unendlich.
Die kubische Spirale wird durch die Länge der Spiralkurve und durch den Radius des anschließenden Bogens definiert. Die Formeln für die Parameter x und y lauten für diese beiden Werte wie folgt:
Parameter x:
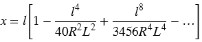
Parameter y:
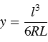
Parameter x:
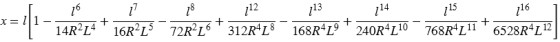
Parameter y:
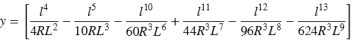
Der Bloss-Übergangsbogen kann nur voll ausgebildet sein, das heißt, für eine Eingangsklothoide ist der Anfangsradius unendlich und für eine Ausgangsklothoide ist der Endradius ebenfalls unendlich.
Diese kubische Parabel wird durch die Länge der Spiralkurve und den Radius des angrenzenden Bogens definiert. Die Formeln für die Parameter x und y lauten für diese beiden Werte wie folgt:
Parameter x:
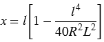
Parameter y:
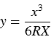
Die Kubische Parabel (Korea) kann nur voll ausgebildet sein, das heißt, für eine Eingangsklothoide ist der Anfangsradius unendlich und für eine Ausgangsklothoide ist der Endradius ebenfalls unendlich.
Die Kubische Parabel (NSW) ist eine besondere Spiralparabel, die für Eisenbahnprojekte in New South Wales (Australien) verwendet wird.Sie ist durch die Länge der Parabel und einen Wert m definiert.Siehe unter NSW Government Technical Note ESC 210 Track Geometry and Stability.