Övergångstyper
Programmet stöder följande spiraler:
| Metod | Längd | Sista station | SP |
|---|---|---|---|
| Klotoid spiral |
* |
* |
* |
| Oval klotoidspiral |
* |
* |
– |
| Kubisk spiral |
* |
* |
* |
| Bloss spiral |
* |
* |
* |
| Koreansk klotoid och PI |
* |
|
* |
| Koreansk kubisk parabel |
* |
* |
* |
| NSW kubisk parabel |
* |
* |
– |
 Klotoid spiral
Klotoid spiral
En klotoidspiral definieras av spiralens längd och radien för den angränsande bågen. Formeln för parametrarna x och y baserat på dessa två värden är följande:
Parameter x:
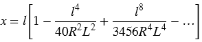
Parameter y:
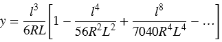
 Oval klotoidspiral
Oval klotoidspiral
Genom att ändra Start / slutradie för en Inåt / Utåtspiral från Oändlig till en spiral där radie krävs är det möjligt att definiera en oval klotoid. För att gå tillbaka till oändlig radie väljer man Oändlig från popup‑menyn.
 Kubisk spiral
Kubisk spiral
Den kubiska spiralen definieras som spiralens längd och radien av den anslutande bågen. Formeln för parametrarna x och y baserat på dessa två värden är följande:
Parameter x:
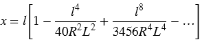
Parameter y:
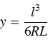
 Bloss spiral
Bloss spiral
Parameter x:
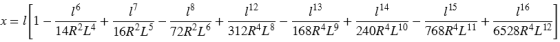
Parameter y:
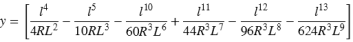
NOTERA – Bloss spiralen kan endast vara helt utveckad. Detta innebär för en ingångsövergång att startradien är oändlig och på samma sätt är slutradien oändlig vid utgångsövergången.
 Koreansk klotoid
Koreansk klotoid
Den koreanska klotoiden är en metod som använder en vanlig klotoidspiral för att definiera en linjegeometri med linjär koncentrisk sektionering. Den definieras med hjälp av Metoden skärningspunkt (PI), där indata inkluderar övergångslängderna för konstruktionens mittlinje och radien för konstruktionens mittlinje. Dessa indata etablerar två koncentriska banor: en mittlinje för mätning och en mittlinje för byggnation. Den vertikala linjegeometrins startpunkt kan definieras antingen av avståndet från början på den horisontella linjegeometrin eller av sektioneringen för den vertikala skärningspunkten (VPI).
 Koreansk kubisk parabel
Koreansk kubisk parabel
En kubisk parabel definieras av parabelns längd och radien för den angränsande bågen. Formeln för parametrarna x och y baserat på dessa två värden är följande:
Parameter x:
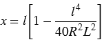
Parameter y:
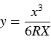
NOTERA – En koreansk kubisk parabol kan endast vara helt utveckad. Detta innebär för en ingångsövergång att startradien är oändlig och på samma sätt är slutradien oändlig vid utgångsövergången.
 NSW kubisk parabel
NSW kubisk parabel
En NSW kubisk parabel är en speciell parabel som används för tågrälsprojekt i New South Wales, Australien. Den definieras av parabelns längd och värdet m. Se NSW Government Technical Note ESC 210 Track Geometry and Stability.