Coordinate system parameters

A coordinate system locates points in two dimensional or three dimensional space. The coordinate system transforms measurements from a curved surface (the earth) onto a flat surface (a map or plan). A coordinate system consists of at least a map projection and a datum.

A map projection transforms locations from the surface of an ellipsoid into locations on a plane or map using a mathematical model. Transverse Mercator and Lambert are examples of common map projections.

Positions on a map projection are commonly called "grid coordinates".

Because an exact model of the earth's surface cannot be created mathematically, localized ellipsoids (mathematical surfaces) have been derived to best represent specific areas. These ellipsoids are sometimes referred to as local datums. NAD‑83, GRS‑80, and AGD‑66 are examples of local datums.

GNSS measurements are referenced to the 1984 World Geodetic System reference ellipsoid, known as WGS‑84. However, for most survey tasks, results in terms of WGS‑84 have little value. It is better to display and store results in terms of a local coordinate system. Before you start a survey, choose a coordinate system. Depending on the requirements of the survey, you can choose to give the results in the national coordinate system, a local coordinate grid system, or as local geodetic coordinates.

In additional to a map projection and local datum, a local coordinate system for a GNSS survey consists of:

  • datum transformation
  • horizontal and vertical adjustments calculated after a site calibration

When WGS‑84 coordinates are transformed onto the local ellipsoid using a datum transformation, local geodetic coordinates result. Local geodetic coordinates are transformed into local grid coordinates using the map projection. The result is northing and easting coordinates on the local grid. If a horizontal adjustment is defined, it is applied next, followed by the vertical adjustment.

To conduct a real‑time survey in terms of local grid coordinates, define the datum transformation and map projection before starting the survey.

GNSS is based on the WGS‑84 ellipsoid, which is sized and positioned to best represent the entire earth.

To survey in a local coordinate system, the WGS‑84 GNSS positions must first be transformed onto the local ellipsoid using a datum transformation. Three types of datum transformation are commonly used. Alternatively, you can choose not to use a transformation at all.

Available datum transformations are:

  • Three‑parameter – This assumes that the rotational axis of the local datum is parallel with the rotational axis of WGS‑84. The three‑parameter transformation involves three simple translations in X, Y, and Z. The three‑parameter transformation that Trimble Access uses is a Molodensky transformation, so there may also be a change in ellipsoid radius and flattening.

    The U.S. State Plane 1927 and the U.S. State Plane 1983 coordinate systems use three‑parameter transformations.

  • Seven‑parameter – This is the most complex transformation. It applies translations and rotations in X, Y, and Z, as well as a scale factor.

  • Datum grid – This uses a gridded data set of standard datum shifts. By interpolation, it provides an estimated value for a datum transformation at any point on that grid. The accuracy of a datum grid depends on the accuracy of the gridded data set it uses.

    A datum grid transformation uses interpolative methods to estimate the value of the datum transformation at any point in the area covered by the datum grid files. Two gridded datum files are required for this interpolation – a latitude datum grid file and a longitude datum grid file. When you export a datum grid using Trimble Business Center, the two datum grid files associated with the current project are combined into a single file for use in the Trimble Access software.

    If you use the Canadian NTv2 datum grid please note the data is provided on an "as is" basis. The Department of Natural Resources Canada (NRCan) makes no guarantees, representations, or warranties respecting the data.

Calibration is the process of adjusting projected (grid) coordinates to fit the local control. A calibration calculates parameters for transforming WGS‑84 coordinates into local grid coordinates (NEE).

You should calculate and apply a calibration before:

  • staking out points
  • computing offset or intersection points

If you calibrate a project and then survey in real time, the General Survey software gives real-time solutions in terms of the local coordinate system and control points.

You can reuse the calibration from a previous job if the new job is completely encompassed by the initial calibration. To copy the calibration from an existing job to a new job, add the existing job as a template in the Project properties screen and then create a new job from the template.

If a portion of the new job lies outside the initial project area, add additional control points to cover the unknown area so that these points can be surveyed and a new calibration calculated.

If published datum transformation parameters are used, slight discrepancies can exist between local control and GNSS‑derived coordinates. These discrepancies can be reduced using minor adjustments. Trimble Access calculates these adjustments during a Site calibration, if the coordinate system settings for the job include a projection and a datum transformation. They are called horizontal and vertical adjustments.

If required, you can use a geoid model file as part of the vertical adjustment calculation.

Trimble recommends that you use a geoid model to obtain more accurate orthometric heights from your GNSS measurements than from the ellipsoid. If required you can then perform a site calibration to adjust the geoid model by a constant value.

The geoid is a surface of constant gravitational potential that approximates mean sea level. A geoid model or Geoid Grid file (*.ggf) is a table of geoid‑ellipsoid separations that is used with the GNSS ellipsoid height observations to provide an estimate of elevation.

The geoid‑ellipsoid separation value (N) is obtained from the geoid model and is subtracted from the ellipsoid height (H) for a particular point. The elevation (h) of the point above mean sea level (the geoid) is the result. This is illustrated in the following diagram:

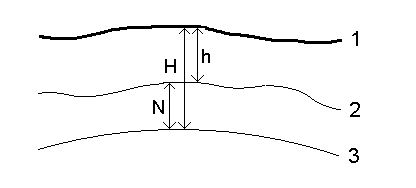
1 – Ground
2 – Geoid
3 – Ellipsoid

For correct results, the ellipsoid height (H) must be based on the WGS‑84 ellipsoid.

When you select geoid model as the vertical adjustment type, the software takes the geoid‑ellipsoid separations from the geoid file chosen, and uses them to display elevations on the screen.

The benefit using the geoid model for the vertical adjustment is that you can display elevations without having to calibrate on elevation benchmarks. This is useful when local control or benchmarks are not available, as it makes it possible to work "on the ground" rather than on the ellipsoid.