About the spectrum analyzer

A spectrum analyzer is a device that displays electronic signals on a screen. The screen is organized with the x-axis as frequency and the y-axis as power, typically in units of dBm (decibels referenced to 1 mW). A spectrum analyzer is similar in function to an oscilloscope, however with an oscilloscope, the x-axis is time and the y-axis is voltage.

So why is a spectrum analyzer necessary? This question is best answered by viewing an example waveform as an oscilloscope would see it and then show what a spectrum analyzer would show.

Consider the following three example signals:

1.0 * sin(1,884,955.6t) volts
2.2 * sin(3,141,592.7t) volts
1.75 * sin(2,733,185.6t) volts

The argument inside the brackets of the above signals is the radian frequency and is known as which is given by 2πf. As such, the frequencies for the above signals are 300 Khz, 500 Khz, and 435 Khz respectively. In this example we will drive all three of these signals directly into the 50 Ω input of a spectrum analyzer and use a 10 MΩ input impedance scope probe to measure the resultant voltage at the spectrum analyzer input. What would be shown on the scope is the thick purple line shown below in Figure 1:

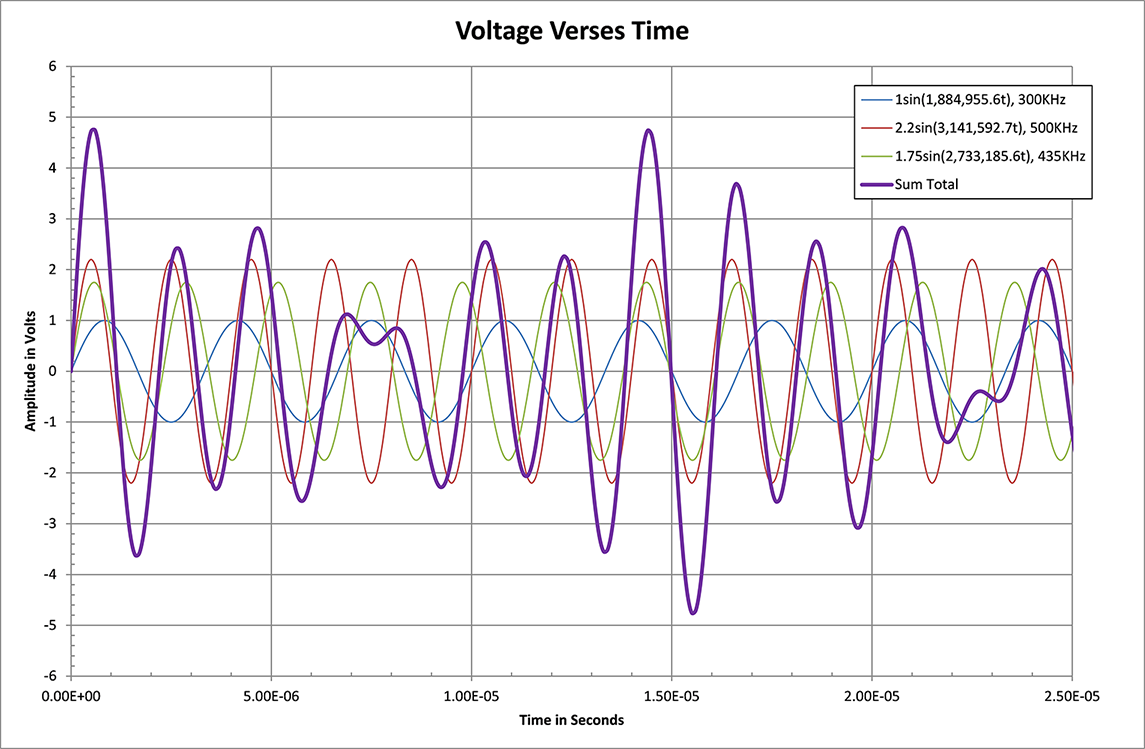
Figure 1

The blue, green, and red curves are the example signals as given above but they will not be visible on a real scope as they are, only the superposition sum of the three signals will be shown on the scope which is the thick purple curve. This thick purple curve shows no evidence of the original signals that comprise it. An observer would not know the frequency or amplitudes of the component signals that the purple curve is made of.

The display that a spectrum analyzer would show of the same thick purple curve from Figure 1, is shown in Figure 2:

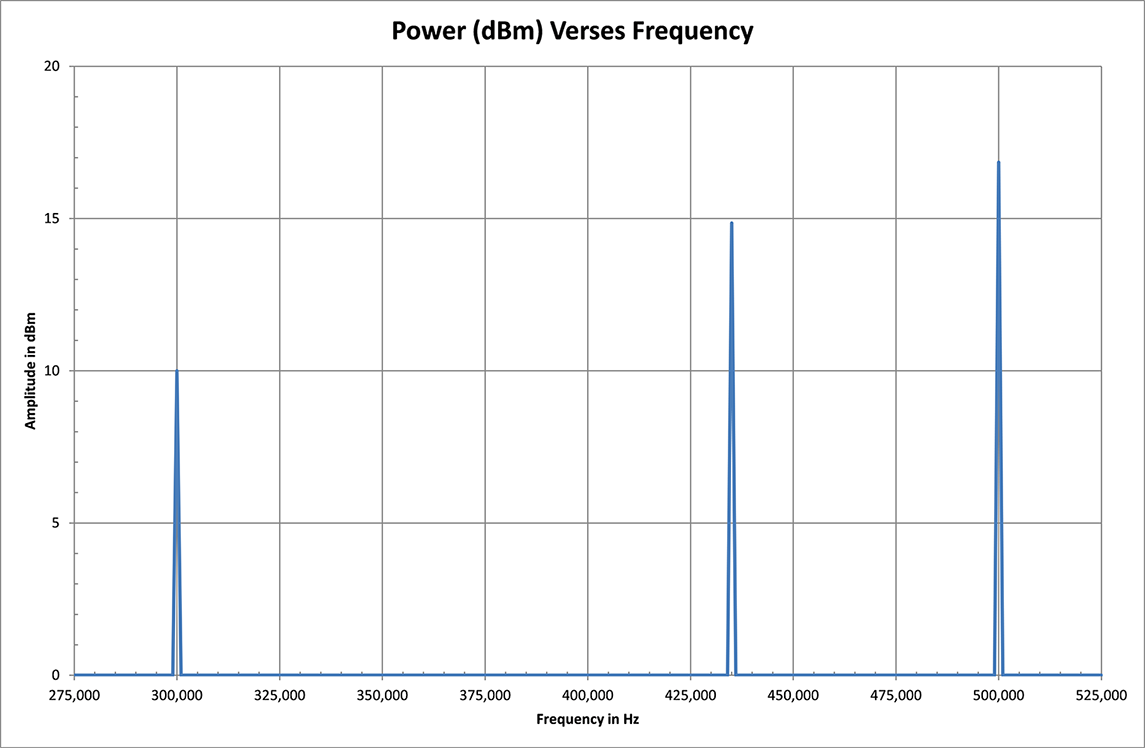
Figure 2

Unlike Figure 1, the horizontal scale on the spectrum analyzer is frequency and not time. The y-axis of the spectrum analyzer shows power in units of dBm whereas Figure 1 shows voltage. Figure 2 clearly shows the three signals' amplitudes and frequency when driven into a 50 Ω load.

Spectrum analyzer amplitudes verses an oscilloscope

The apparent difference in amplitudes shown in Figures 1 and 2 can be confusing. To illustrate that the signals in Figure 2 are actually the original example signals, the first signal will be looked at. Signal one has a peak voltage of 1 Vp. To compute the power this will have to be converted to a rms value which is 0.707*Vp or 0.707 Vrms. The voltage is being driven into a 50 Ω load (which is actually the spectrum analyzer input). To compute the power dissipated by this load, the rms voltage must be squared and this square divided by the resistance (50 Ω) which yields 10 mW. This 10 mW must then be converted to dBm by first dividing by 1 mW (resulting in a value of 10), taking the base 10 log (resulting value of 1) and then multiplying by 10. This yields a result of 10 dBm which is exactly what is shown in Figure 2 at 300 Khz.

Spectrum analyzer summary:

Shows amplitudes in dBm not volts
Shows amplitudes verses frequency not time
Shows the amplitudes referenced to 50 Ω